零の発見　－数学の生い立ちー

1939年初版

吉田洋一　著

内容

インドにおける０（ゼロ）の発見は約6世紀頃と推定され、その後アラビアを経由して千年ほどかけてヨーロッパに広まり、数学と計算法が発展することとなった。またギリシャ哲学から始まる直線という「連続」の問題に対する数学的なアプローチの歴史についても平易に説明する。

☆☆☆

「二度つけ禁止」

でかでかと貼られた無粋な注意書きをしり目に、添えてあるキャベツをスプーン代わりに私は串カツにソースを垂らす。

これでつけすぎることなく、自分の分量でソースを加減して食べられるというものだ。

他にもごまだれソース、タルタルソースなどというものも並んでいる。こちらはお好み焼きのマヨネーズの入れ物みたいな振りかけるタイプの容器に入っている。全部これにしてくれればよいのに。薄いハイボールをあおりながら私は考えていた。

「学校の勉強なんてホント役に立たないよね」

どうしてそのような話になったのかは覚えていないけれど、子どもの話だか、そんなことが話題になって、いつの間にか教育論になっていた。

私以外年若い人々であったので、まぁゆとり教育世代なのだと思っていたら、ゆとり教育というのは1980年頃から始まった制度のようである。そして1995年から完全週休二日制となり、学習指導要領も大幅に改定されたようだ。

その中の一人、がっつりゆとり教育を受けた人が眉間にしわを寄せて、吐き捨てるように言う。

「大体、数学とか、歴史とか、全然使わないというか、関係ないじゃん。そういうのにさー、一生懸命になれって言う方がおかしくない？」

「中学とか、高校とかにやりたい事見つけて、それに時間と労力集中した方が絶対いいよ。」

まぁ、確かにそうだよな、と思いながらふんふんと聞いていた。

今も昔も日本の教育なんて「受験」という目標を設定して、それに向かって暗記すべき物事をバリバリと暗記して、消化していくだけというものなのだから、そんなの役に立つわけないし、受験を通過したらきれいさっぱりデリートされてしまう。

ゆとり教育というのは、そういう「ただ消化されるだけ」という教育を止めよう、という趣旨の下に作られたはずなのだけれど、ゆとり教育を受けた人々が「いらない」といっているのだから、それは失敗したのだろう。

「だからさ、勉強とかやりたくない人はやらなくていいんだよ。必要ないね」

なんとなくその言葉は引っかかった。

「必要ないか・・・」

串カツも少なくなってきたし、何か注文しようか、それともこの氷だらけの薄いハイボールを日本酒にしてやるか迷った。

☆☆☆

吉田洋一氏の「零の発見」を読んだのは学校を出て随分経ってからのことだった。

梅田の茶屋町のかっぱ横丁にまだ古本屋が並んでいた頃で、通勤時に読む本を探していた時に見つけたのだ。1979年に発売されたもので、紙も茶色く変色して古本の匂いがした。

岩波新書だからちょっと小難しいだろうと思っていたのだけれど、予想外に面白いというか、ちょっとしたカルチャー・ショックであった。

０（ゼロ）は元々存在していなかったこと、そこに辿り着くまでに人類が紆余曲折経てきた経緯などは単純に「へー！」と驚いたし、さらに疑問が湧いてくる。古代の人は０（ゼロ）なしにどうやってあんな建築物を建てたりしていたのだろうか？

そこからさらにピタゴラス、ギリシャの哲学者や、幾何学の話になっていくのであるが、ここからこの本の評価の分かれ道になるというか、ちょっと難解になってきて、大学の講義チックになってくる。

しかし、面白いのはなんと言ってもピタゴラスの話だ。

話は逸れるのだが、少し前に「ダヴィンチ・コード」という小説が流行り、映画にもなった。そこに出てくるのがフリーメイソン、イルミナティという言葉だ。このインターネット時代、陰謀論、都市伝説、みんな大好きで一度は耳にしたことがあると思うのだが、そのイルミナティの源流は「ピタゴラス」を教祖とするピタゴラス教という説もある。

☆☆☆

ピタゴラスは紀元前570年頃イオニアのサモスで生まれた。後に僭主政治を嫌いイタリアに移り、クロトンに学園を作った。かの有名な哲学者の学校ということで、内外の富裕な家の子弟が争ってピタゴラスの門に入ることになった。

ピタゴラスは哲学者であると同時に霊魂の不滅と輪廻を説く神秘的な宗教家でもあった。この学園＝教団では、一種の戒律生活がまもられた。輪廻の苦しみを逃れるために魂をきよめることがその目的であった。それと同時に算術、音楽、幾何学、天文学の四科を学び、宗教と密接に結びつけた。

なかでも最も重要視していたのが算術であり、天文学、幾何学的図形との融合は宇宙の調和を啓示するものとして「万物は数である」という思想を生み出した。

この時、ピタゴラスが念頭に置いていた「数」とは「自然数」のことだったという。

自然数とは物を数える時に使う「１、２、３、、、」といった正の数のことで、この自然数で表されるのが宇宙の調和ということになっていた。

ところが、かの有名な「ピタゴラスの定理」というものが発見されたのである。

直角三角形をなす3編のうち、2辺の長さを知ることができれば、残り１辺の長さを知ることができる三平方の定理。

中学生の時やりましたね。

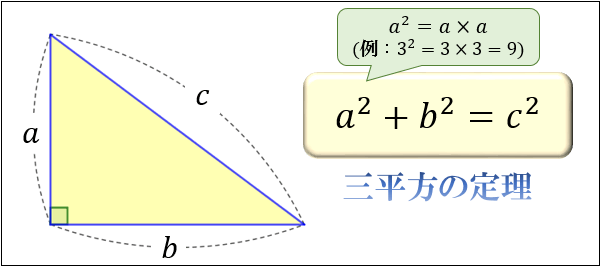
これを発見したピタゴラス一門はこの定理の持つ美しさ鮮やかさに驚嘆し、これまでの調和的世界観が正しい概念であったと、さらに確信を深めた。

しかしこれは同時に調和に充ちたピタゴラスの世界に波紋を起こすパンドラの箱に他ならなかった（パンドラの箱開けちゃったよね）。

―直角三角形の斜辺の平方根を求めると、ほとんどの場合自然数とはならない。

一番分かりやすい例は直角を挟む二辺の長さが等しい場合である。

いわゆる直角二等辺三角形。

１辺を仮に１とした場合、その斜辺は２の平方根だから√２になってしまう。

習いましたね。ヒトヨヒトヨニヒトミ・・・1.414213・・・となる。

要するに自然数で表すことができないのだ。

かくして、ピタゴラスとその弟子たちはこれによって苦悩し、また時の権力者に危険視されて教団は解散を余儀なくされ、ピタゴラスは流浪の末、８０年という生涯を閉じた。・・・

☆☆☆

「二等辺三角形の斜辺を求める場合、大体テストに出てくるパターンは１辺が１だから斜辺は√２と覚えておけ。」

私が学校で受けた授業はこのたった１行である。

この三平方の定理に、ピタゴラスの人生を狂わすようなドラマが隠されていたと、もし中学生の時に知っていたとしたら、もしかしたら数学が好きになっていたかもしれない。いや、好きになっていたでしょ。

学校の先生を責めるつもりはないが、これが詰め込み教育というものである。

最近は哲学科とか人文科学系を廃止して、理系に特化した大学に助成金が多く支払われるという制度ができたようで、どんどん文系の学部が減っているようだ。また、国語の授業に「論理的に文章を読む」、という項目が追加されて、取扱説明書とか、法律の文章などを読ませる授業が始まったらしい。例えば入試に「駐車場の使用契約書」を読ませ、貸し手が急な値上げを通告してきた場合にどの条文の、どんな点について質問すべきかを尋ねる、といった問題が出るということである。

「二度づけ禁止」

この注意書きの場合、過ちではないものを選べ。

１　キャベツでソースをすくって串カツにかけた場合

２　衣を外して中身だけつけた場合

３　隣のテーブルのソースにつけた場合

こういうことを学校で「勉強」するのだろうか？

周りの人々はもう話題を変えて、ハイボールと同じくらい薄い話題で盛り上がっているフリをしていた。私は追加注文をやめて、ひとまずみんなに挨拶をし、次の店には行かずに電車に乗った。

どんな話題もきっとみんなあまり興味がないのだろう、と思った。

ふと、必要ないことに一所懸命で、馬鹿馬鹿しいほど熱くなっていた頃が懐かしくなった。

文責；Y